随机数最初被应用在密码学里,计算机出现后被广泛应用于计算机编程领域。从简单的短信验证码、幸运转盘、随机播放音乐、棋牌类游戏中的随机洗牌,到安全登录、使用随机密钥进行数据加密等,都会用到随机数。在这篇文章里,我们就来介绍一下计算机里的随机数,以及真随机数与伪随机数。本文内容包含以下几个部分:
1. 什么是随机数
2. 真随机数与伪随机数
3. 为什么使用伪随机数,而不是真随机数
4. 如何生成伪随机数
5. 如何生成真随机数
6. 真随机数或伪随机数很重要吗
7. 有时候,可能并不需要真随机数
8. 随机数偏差:赌徒谬误
9. 蒙特卡洛方法使用随机数求 π
1. 什么是随机数
很多人都玩过掷骰子的游戏,通过掷骰子的方式生成的点数,就是一个 1 到 6 之间的随机数。随机数可以简单理解为随机的数字,是从一组可能的值中提取出来的,并且每个可能的值被提取的概率是一样的。这也是随机数的基本特点:随机性。除了随机性,真正的随机数还需具备另外两个特点:不可预测性和不可重现性。
- 随机性:不存在统计学偏差,是完全杂乱的数列
- 不可预测性:不能从过去的数列推测出下一个出现的数
- 不可重现性:除非将数列本身保存下来,否则不能重现相同的数列
2. 真随机数与伪随机数
同时满足上面三个条件的随机数就是「真随机数」(true random numbers)。前面提到的掷骰子,产生的数就是真随机数,因为它产生的数列同时具备随机性、不可预测性、不可重现性三个特点。
有真随机数就有假随机数,也就是「伪随机数」(pseudorandom numbers)。具有随机性但又不能满足上面所有条件的都被归类为伪随机数。而伪随机数又分两种:其中只有随机性特点的伪随机数被称为「弱伪随机数」,有随机性同时又有不可预测性的伪随机数被称为「强伪随机数」。
在一些对安全级别要求不高的随机数应用场景中(如短信验证码、幸运转盘),可以使用弱伪随机数。而在一些安全级别要求较高的场景中,如使用随机密钥进行数据加密时,就需要使用强伪随机数甚至真随机数,这样可以提高加密过程的不可预测性,从而增加破解难度。
平时我们接触到的计算机里使用的随机数都是伪随机数。下面是一个使用真随机数与伪随机数生成位图的比较。图片左侧使用的是真随机数(random.org 数据),右侧使用的则是计算机中的随机数(PHP rand 函数生成的伪随机数)。可以看到计算机里的伪随机数具有不那么随机(具有明显周期性)的特点。

3. 为什么使用伪随机数,而不是真随机数
既然真随机数比伪随机数更随机,为什么还需要使用伪随机数呢?简单来说就是随机数越是接近真随机数,生成的成本越高。
首先一般的计算机根本无法生成真随机数。计算机里生成随机数的方法都是首先获取一个种子数字(如计算机时间),然后将这个数字通过某种算法经过一系列运算从而得到随机数,同时这个随机数又会作为下一个随机数的种子数字。但不管采用什么算法,都无法满足不可重现性这一特点。因为只要后面的数字与前面出现过的数字相同时,后面生成的随机数列也会是相同的。
而要生成真随机数,除了算法还需要借助一些特殊硬件在算法中加入其它一些随机因子。如在服务器上使用可以获取服务器本身热噪声数据的硬件设备。
并且越是接近真随机数,生成过程所花费的时间会越长,因为这通常意味着需要使用更复杂的算法进行更多的运算。这也是很多场景里使用伪随机数,甚至是弱伪随机数的一个重要原因。
4. 如何生成伪随机数
下面以生成随机数最基础的方法「线性同余法」(Linear congruential generator)为例,看一下如何生成一组随机数。
线性同余法使用下面的递归公式来生成随机数列:

其中 a、c、m 是三个设定的常数。用 a 乘以上一个随机数,与 c 相加,最后与 m 求余,从而得到下一个随机数。在算第一个随机数时,上一个随机数还不存在,需要指定一个数字,这个数字被称为种子数字(seed)。
线性同余法的周期(也就是出现两个相同随机数的间隔)最大为 m,因为任何数与 m 取余的结果都是一个位于 0 与 m - 1 之间的数字,最多递归到第 m 次必然出现与前面出现数字重叠的现象。而通过这个算法也可以看到,只要出现一个重复的数字,后面出现的所有数字序列与前面出现的序列都是重叠的。而大部分情况下线性同余法的周期都会小于 m。要令线性同余法达到最大周期 m,a、c 以及 m 三个常数数值还应符合以下条件:
- c 与 m 互质
- m 的所有质因数都能整除 a - 1
- 若 m 是 4 的倍数,则 a - 1 也是
- a、c、以及种子数字都比 m 小
- a、c 是正整数
可以通过两个 a、c、m 不同取值的例子,看一下取值对这个算法的影响。
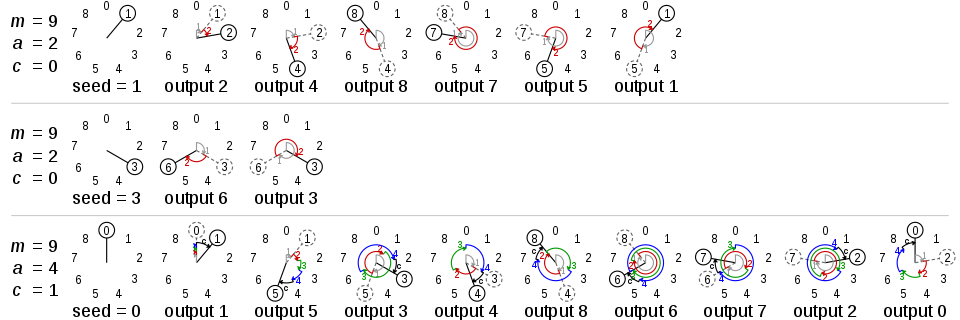
通过上面的结果可以看到,当 m = 9, a= 2, c=0 时,生成随机序列的周期依赖种子数字(seed)的取值。当种子数字为 1 时,可以生成一个周期为 6 的随机序列;而当种子数字为 3 时,随机序列的周期仅为 2,仅能生成值为 6 或 3 这两种数字。而当 m = 9, a= 2, c=1 时,不管种子数字是多少,都可以生成一个周期为 9(最大周期)的随机序列。
在实际计算机生成随机数的算法里,m 会取一个很大的数字(如 2^32,2 的 32 次方),同时严格选择 a 与 c 的值,这样可以使生成的随机数列周期很大(接近 m 值)。但不管怎样,算法总会在某个时刻重复出现前面重复出现过的数字,并且在这个数字后面的所有数字都会与前面出现的部分重复。这也是我们说平时我们接触到的计算机里使用的随机数都是伪随机数的原因。
5. 如何生成真随机数
要在计算机里生成真随机数,除了算法方面还需要借助一些特殊的硬件在算法中加入其它一些随机因子。这些随机因子可以是用户键盘或鼠标相关的随机操作数据,也可以是环境噪音、计算机本身热噪声、宇宙射线、放射性同位素衰变数据等任何在物理层面产生的随机数据。
现在某些计算机 CPU 里可以通过放大电路的热噪声并以此为因子来产生真随机数。我们知道温度高于绝对零度的原子都存在热运动,在集成电路里这些原子的热运动会在电路里产生噪声,噪声会使得电路中的电压存在微小的起伏,而这些起伏变化是可以视为随机的。这种 CPU 正是通过获取这些变化的随机数据并以此来生成真随机数。
但这种真随机数也有明显的缺点,那就是生成的速度比我们上面提到的伪随机数会慢很多。通常这种真随机数只被用在一些对安全级别要求较高的场景中,如使用随机密钥进行数据加密时,用来提高加密过程的不可预测性,增加破解难度。
6. 真随机数或伪随机数很重要吗
对于一些如打乱音乐播放列表或在触发一个游戏事件时挑选一个随机样本的一般场景里,使用的究竟是伪随机数还是真随机数其实无关紧要。在这些场景中,是不是接近真随机数对一般用户来说区别并不是很大。
在某些场景中,使用伪随机数还可能是更好的选择,比如为某些科学研究挑选一个随机样本时,使用伪随机数能让其他人通过使用同样的种子数字值来复现你的研究。在一些游戏开发领域,在测试游戏时能够复现同样的「随机」事件反而会带来更多便利。
而在另外一些场景中,需要使用真随机数,或使用随机性相对较高的随机数如强伪随机数。如在数据加密相关应用中,使用真随机数是非常重要的,因为这有助于数据的持续保护。另外在一些棋牌类游戏或博彩类应用中增加相关随机性也可以有效降低各种作弊可能。
7. 有时候,可能并不需要真随机数
关于随机数,有些时候真随机数并不一定是人们的所预期的「随机数」。以下面这张图里的左右两部分为例 —— 你觉得其中哪个部分是真正的随机分布,哪个部分又是刻意营造的随机分布?

很多人会认为右边黑点的分布看起来更随机一些。但其实右边的部分为了确保黑点的均匀分布经过了调整,是可以营造的效果。事实上,左边的部分才是真实随机分布的结果。而这种真实随机分布的结果有时却并不一定符合我们的直观预期。
在线数字音乐服务 Spotify 曾经有这样一个案例。多年以来,Spotify 用户一直在抱怨随机音乐播放列表的随机效果并不是很随机,他们认为 Spotify 的随机算法有问题。Spotify 调查了这个问题,发现他们的算法的确是随机的,但问题是越是随机,同一位艺术家的音乐越有可能会被一首接一首地播放。而这显然不符合用户对随机的预期。为了解决这一问题,Spotify 在算法中降低了随机性,使得来自同一艺术家的音乐在播放列表中刻意被分开,使其更符合人们心目中随机性。
8. 随机数偏差:赌徒谬误
正像上面例子我们看到的,人们期望的随机性与真实的随机性之间并不总是一致。这种偏差现象又被称为「赌徒谬误」(gambler’s fallacy)。就像掷硬币时,如果连续出现十次正面,人们往往会相信第十一次掷出背面的概率会大一些,但事实却不是这样。
赌徒谬误可以总结为下面两点:
- 相信独立随机事件(比如掷硬币、掷骰子)具有某种固有的趋向于平均值的性质。就像掷硬币时,如果出现了连续正面朝上的情况,就相信背面朝上的可能性会增大,因为这样可以让正面背面出现的比率更接近平均值。
- 人们往往低估独立随机事件连续发生的可能性。一个常见的现象是轮盘赌桌上的人在看过之前结果的列表后,如果看到连续出现了五个黑色数字,就会相信下一个数字为红色的可能性会更高,从而低估黑色数字连续出现的可能性。
假设轮盘每天转 12 小时,平均每分钟转一次,那么每天就能转 720 次。假设出现红色数字和黑色数字的概率都是 50%(为了简单起见,忽略其他情况),你认为一天里连续出现 8 次或更多次黑色或红色数字的概率是多少?
答案是大于 75%。换句话说,平均四天中有三天都会出现至少一组 8 次或更多次的黑色或红色数字连击。不仅如此,每天还有 30% 的几率出现至少 10 次的连击,而出现 12 连击的概率大约为 8%。而这显然与多数人预期的结果是不一样的。
9. 蒙特卡洛方法使用随机数求 π
蒙特卡罗方法是一种以概率统计理论为指导的数值计算方法,可以通过随机数(伪随机数)来解决很多计算问题。
比如近似计算圆周率,方法为:
- 每次随机生成两个 0 到 1 之间的随机数,检查以这两个数为横纵坐标的点是否落在单位圆内
- 生成一系列随机点,统计落在单位圆内点数个数与总点数之间的比率
而理论上单位圆内的点数个数与总点数的比率应该近似于四分之一圆面积与正方形面积的比率,即:π:4 。通过这样的关系我们就可以使用随机数来近似的求出 π 值。
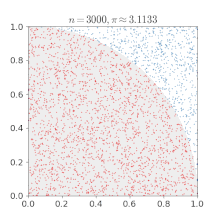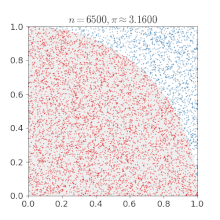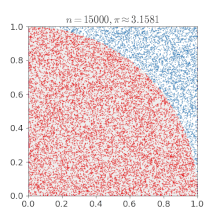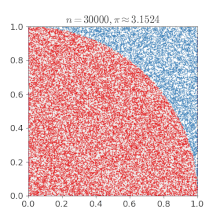
在 C 语言中的实现代码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(int argc, char* argv[]) {
int times = 100000, sum = 0;
srand(time(0));
for (int i = 0; i < times; ++i) {
double x = (double) rand() / RAND_MAX;
double y = (double) rand() / RAND_MAX;
if ((x * x + y * y) <= 1.0) {
sum++;
}
}
double pi = 4.0 * sum / times;
printf("pi = %f", pi);
return 0;
}
了解更多少儿编程相关科普文章,请参考:
少儿编程之计算思维的新定义:计算思维是我们想要最小化的摩擦,除非它是生成的
少儿编程之编程思想介绍 —— 思想,作为一种技术
少儿编程之 Kill Math 项目介绍:让数学不只是符号
少儿编程之 Dynamicland 项目介绍:可视空间与设计工坊
少儿编程之二进制:计算机二进制的历史,二进制与十进制的转换及相关亲子互动游戏
少儿编程之随机数:计算机里的随机数,真随机数与伪随机数
了解更多家庭教育方面的信息,请参考:
家庭教育方法:关于儿童如何学习的背景思考
决定孩子成功的关键是什么?家长应该注重孩子哪些特质的培养?对于孩子的学习,家长应该更注重结果,还是过程?
青少年必备书单:最适合孩子阅读的 100 本经典图书;少儿书单;儿童必读书籍;少儿图书推荐;青少年必读图书
扫码下面二维码,关注我们的公众号,阅读最新文章或观看更多视频教程:


